塔勒布系列《随机漫步的傻瓜》第2章书评
 2162
2162第二章——奇特的结算方法
【精彩片段】
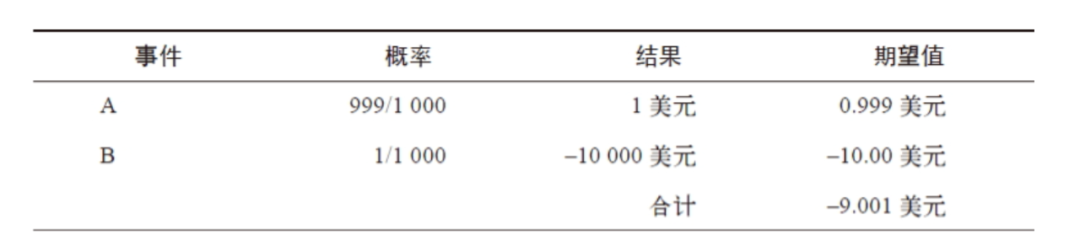
我举的例子会同时提到不对称概率和不对称结果。不对称概率是指每一事件的概率不是50%,而是一边的概率高于另一边的概率。不对称结果是指报酬不相等。假设我参加的赌博,1000次里面有999次赚到1美元(事件A),有一次赔10000美元(事件B),如表6–1所示。我的期望值是赔9美元左右,这是将概率乘以对应的结果所得到的数字。赔钱的频率或概率本身完全没有用处,它必须和结果的大小一起判断。这里的A发生的概率远高于B。我们如果赌事件A会发生,赌赢的概率很高,但这么做不是好想法。
他们怎么会不懂其中的道理?他们怎么会把概率和期望值混为一谈,也就是把概率和概率乘以报酬混为一谈?主要是因为大多数人接受的学校教育、举的例子都是出现在对称的环境中,例如掷硬币时,这种差别就无关紧要。事实上,社会中应用甚广的所谓“钟形曲线”是完全对称的,后面我会再谈这一点。
所以这就是奇怪的结算方式:牙医的1000万为什么比赌博的1000万性质不一样?因为同样是1000W,牙医的期望值更高。
一次性赚大钱不是本事,持续盈利才是本事。
或者说,一次盈利本来就是half to half的概率事件,如果能持续盈利,就是小概率事件。而能将小概率事件变成必然的才是真本事。不幸的是,俄罗斯转盘每次赌对都是靠运气,不是靠真本事。
放在跨境电商上,上面有条评论已经阐述过了,这里不再赘述。
【Lee点评】
Anyway, 希望你是正确的。
因为这本书真的很贵。
【精彩片段】
就像你是BSR,也许你的图片文案并不怎么高明,只是做得早而已,但依然会引导类目竞品的风向,并被奉为圭臬。无他,你已经拿到话语权了。
就像别人是销冠,Ta上班看手机是为了查看竞品动态,你上班看手机就是摸鱼。
话语权运用之妙存乎于心,愿我们不是那沉默的大多数。
需要补充的是,在作者这里,这句话有别的含义,Lee属于歪解了。后面在非对称性风险里,我们会继续谈到风险和业务兼于一身的好处。


























第二章——奇特的结算方法
【精彩片段】
我举的例子会同时提到不对称概率和不对称结果。不对称概率是指每一事件的概率不是50%,而是一边的概率高于另一边的概率。不对称结果是指报酬不相等。假设我参加的赌博,1000次里面有999次赚到1美元(事件A),有一次赔10000美元(事件B),如表6–1所示。我的期望值是赔9美元左右,这是将概率乘以对应的结果所得到的数字。赔钱的频率或概率本身完全没有用处,它必须和结果的大小一起判断。这里的A发生的概率远高于B。我们如果赌事件A会发生,赌赢的概率很高,但这么做不是好想法。
他们怎么会不懂其中的道理?他们怎么会把概率和期望值混为一谈,也就是把概率和概率乘以报酬混为一谈?主要是因为大多数人接受的学校教育、举的例子都是出现在对称的环境中,例如掷硬币时,这种差别就无关紧要。事实上,社会中应用甚广的所谓“钟形曲线”是完全对称的,后面我会再谈这一点。

所以这就是奇怪的结算方式:牙医的1000万为什么比赌博的1000万性质不一样?因为同样是1000W,牙医的期望值更高。
一次性赚大钱不是本事,持续盈利才是本事。
或者说,一次盈利本来就是half to half的概率事件,如果能持续盈利,就是小概率事件。而能将小概率事件变成必然的才是真本事。不幸的是,俄罗斯转盘每次赌对都是靠运气,不是靠真本事。
放在跨境电商上,上面有条评论已经阐述过了,这里不再赘述。
【Lee点评】
Anyway, 希望你是正确的。
因为这本书真的很贵。
【精彩片段】
就像你是BSR,也许你的图片文案并不怎么高明,只是做得早而已,但依然会引导类目竞品的风向,并被奉为圭臬。无他,你已经拿到话语权了。
就像别人是销冠,Ta上班看手机是为了查看竞品动态,你上班看手机就是摸鱼。
话语权运用之妙存乎于心,愿我们不是那沉默的大多数。
需要补充的是,在作者这里,这句话有别的含义,Lee属于歪解了。后面在非对称性风险里,我们会继续谈到风险和业务兼于一身的好处。


 热门活动
热门活动 








 浙江
浙江 03-12 周四
03-12 周四
 热门报告
热门报告 










